Kinematika gerak

Gerak Melingkar Berubah Beraturan

Seperti pada pembahasan gerak lurus, pada gerak melingkar juga dikenal gerak melingkar berubah beraturan (GMBB). Jika perubahan percepatan searah dengan kecepatan, maka kecepatannya akan meningkat. Jika perubahan percepatannya berlawanan arah dengan kecepatan, maka kecepatannya menurun.

Percepatan Total pada Gerak Melingkar Berubah Beraturan (GMB)

Pada gerak melingkar beraturan (GMB), walaupun ada percepatan sentripetal, kecepatan linearnya tidak berubah. Mengapa? Karena percepatan sentripetal tidak berfungsi untuk mengubah kecepatan linear, tetapi untuk mengubah arah gerak partikel sehingga lintasannya berbentuk lingkaran. Pada gerak melingkar berubah beraturan (GMBB), kecepatan linear dapat berubah secara beraturan. Hal ini menunjukkan adanya besaran yang berfungsi untuk mengubah kecepatan. Besaran tersebut adalah percepatan tangensial (at), yang arahnya dapat sama atau berlawanan dengan arah kecepatan linear. Percepatan tangensial didapat dari percepatan sudut (α) dikalikan dengan jari-jari lingkaran (r).

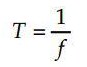
a_t: percepatan tangensial (m/s²) 

α : percepatan sudut (rad/s²)

r : jari-jari lingkaran dalam cm atau m 

Pada Gerak Melingkar Berubah Beraturan benda mengalami dua macam percepatan, yaitu percepatan sentripetal (a_s) dan percepatan tangensial (a_t). Percepatan sentripetal selalu menuju ke pusat lingkaran, sedangkan percepatan tangensial menyinggung lingkaran. Percepatan total dalam GMBB adalah jumlah vektor dari kedua percepatan tersebut.

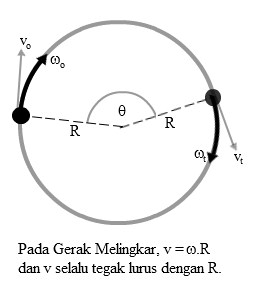
Pada GMBB benda mengalami percepatan sentripetal dan percepatan tangensial.

Berdasarkan gambar di atas, diketahui bahwa percepatan sentripetal dan percepatan tangensial saling tegak lurus. Oleh karena itu, percepatan totalnya adalah sebagai berikut.

Sedangkan arah percepatan total terhadap arah radial, yaitu θ dapat dihitung dengan perbandingan tangen.

 

Rumus Gerak Melingkar Berubah Beraturan

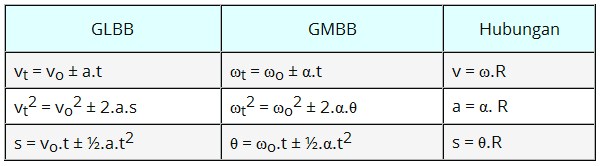
Rumus-rumus yang digunakan dalam GMBB tidak jauh berbeda dengan rumus-rumus dalam GLBB. Jika anda sudah menguasai rumus GLBB, maka rumus GMBB pasti dapat dengan mudah anda pahami. Untuk itu, berikut ini disajikan tabel perbandingan rumus GLBB dan GMBB.

Keterangan :

(+) → benda mengalami percepatan

(−) → benda mengalami perlambatan.

Dengan : 

ω_t = kecepatan sudut setelah t detik (rad/s)

ω_o = kecepatan sudut awal (rad/s)

α = percepatan sudut (rad/s²)

θ = sudut tempuh (radian)

t = waktu yang dibutuhkan (s)

R = jari-jari lintasan (m)

Kecepatan sudut juga sering dinyatakn dalam satuan ppm (putaran per menit) ataupun rpm (rotasi per menit). Satuan tersebut menyatakan banyakanya putaran yang dilakukan benda dalam satu menit. Hubungan satuan tersebut dengan rad/s adalah : 1 ppm = 1 rpm = π⁄30 rad/s

Contoh Soal Gerak Melingkar Berubah Beraturan

Sebuah benda berotasi dengan kecepatan 120⁄π ppm. Jika setelah 10 detik benda tersebut berhenti, maka hitunglah besar sudut yang ditempuh benda tersebut.

Pembahasan :

Dik : ω_o = 120⁄π ppm = 120⁄π (π⁄30) = 4 rad/s; t = 10 s; ω_t = 0.

Karena ω_t < ω_o, maka benda diperlambat.

ω_t = ω_o − α.t

⇒ 0 = 4 − 10α

⇒ 10α = 4

⇒ α = 4⁄10

⇒ α = 0,4 rad/s²

Maka sudut tempuhnya adalah :

ω_t² = ω_o² − 2.α.θ

⇒ (0)² = (4)² − 2.(0,4).θ

⇒ 0 = 16 - 0,8 θ

⇒ 0,8 θ = 16

⇒ θ = 16⁄0,8

⇒ θ = 20 radian.